二次関数の最大・最小問題をパターン別に徹底解説！！！

二次関数の最大・最小問題は、とにかくグラフを書いて視覚的に理解していくことが大事です。

ここでは主に大学入試で出題されるであろう二次関数の最大・最小問題の5つのパターンとその解き方を、例題とともに詳しく解説していきます。

 

一番簡単なパターン

期末テスト等であれば出される可能性のあるレベルの問題です。まずはこの問題を通して、最大・最小問題とは何かを把握していきます。

・解説

まずはグラフを書いてみます。この二次関数を平方完成すると $y=(x-2)^2+1$ が得られるので、この二次関数は頂点 $(2, 1)$ を持つ下に凸のグラフであることがわかります。

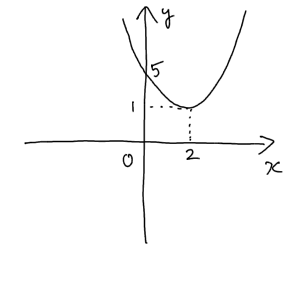
グラフを書けば、どこが最小値でどこが最大値なのかが一発でわかりますよね。グラフより、答えは

$x=2$ で最小値 $1$ 、最大値はなし

となります。最大値に関しては無限に発散するので、特定の値を持たないですから、こういうとき最大値は無しと言います。

そして解答の書き方なのですが、最大値・最小値をとるときの $x$ の値も同時に記入しておいたほうが良いです。→「 $x=2$ で最小値 $1$ 、最大値はなし」こんなふうに。作法としてそうすべき、とされているようなので。

こんな感じで、二次関数の最大・最小問題はとにかくグラフを書いて視覚的に確認しながら問題を解き進めるのがよいです。

では次の問題に行きます。

 

定義域があるパターン

・解説

まずは平方完成して

$y=-2(x-3)^2+7$

グラフを書いて

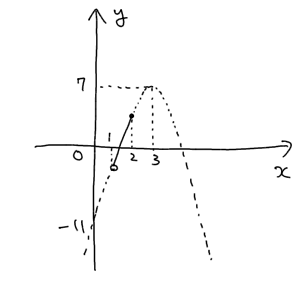
今回の問題では定義域が与えられているので、定義域に注目してみます。この定義域の中での最大値・最小値を求めればいいわけですから、答えは

$x=2$ で最大値 $5$ 、最小値は無し

となります。最小値についてですが、不等号でイコールが入っていない場合でも特定の値を取ることができないので、この場合もやはり最小値は無しとなります。

どんどん次の問題に参りましょう。

 

グラフが動くパターン

ここから急激に面倒くさくなってきます。そしてこれくらいのレベルが実際の大学入試で出されるような問題です。

特にセンター試験ではこの手の問題がよく出てきますので、面倒ではありますが絶対にマスターしておきましょう。グラフを書けば確実に理解できます。

・解説

まずは平方完成します。

$f(x)=\left\{x-(a+1)\right\}^2-a^2-2a-1$

頂点が $(a+1, -a^2-2a-1)$ であることがわかったので、グラフを書いていきます……と言いたいところですが、$a$ ってどこだよ！という話になってしまい、グラフが書けません。

グラフが書けないんだったらもういいよ！帰るよ！となってしまいそうですが、ちょっと待ってください。

この問題で聞かれているのはあくまで最大値と最小値なんです。そしてその値を $a$ で表せばいい。つまり $a$ の値そのものは別に関係ないのです。

そして「最大値と最小値を求める」ということにのみフォーカスして考えると、頂点の存在する位置を場合分けをして考えることによって、最大値と最小値が $a$ の式で表せることがわかります。

具体的に説明していきましょう、まずは最大値を例にして考えてみます。

 

最大値

最大値を求めるにあたっては、頂点が定義域の中点よりも左にあるか右にあるか、の二通りで場合分けをします。なぜかというと、定義域の中点を境にして、最大値が二通りの値を取りうるからです。

・頂点が定義域の中点よりも左側にある場合→定義域の右端が最大値

・頂点が定義域の中点よりも右側にある場合→定義域の左端が最大値

これをグラフで書いて確認していきます。

 

例：頂点が定義域の中点より左にある場合

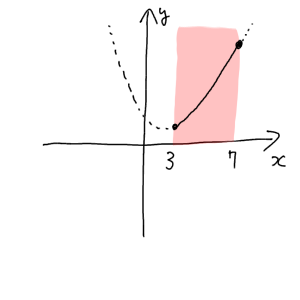
このグラフの最大値に着目してください。頂点が定義域の中点（$x=5$）より左にある場合、ちょっと左にあろうが、メッチャ左にあろうが、いずれにせよ最大値は $x=7$ の点である $f(7)=-14a+35$ として表すことができるんです。

頭の中でグラフを移動させてイメージしてみて下さい。ちょっと左に移動させても、メッチャ左に移動させても、最大値は同じく $x=7$ の点であることが確認できると思います。

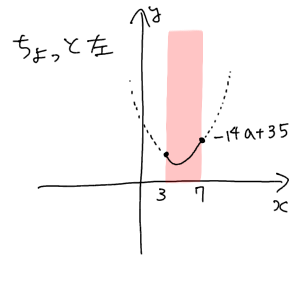
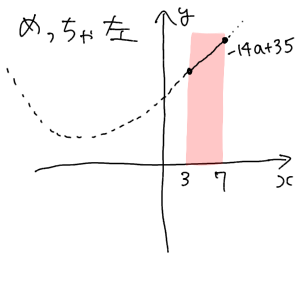
グラフを移動させると、たしかに最大値の位置も変わります。しかし問題で求められているのはあくまで最大値の $a$ の式です。最大値が $-14a+35$ であるという事さえ分かっていればそれで良いのです。

なので、頂点が定義域の中点よりも左にある場合、最大値は常に $-14a+35$ 。ここまで分かれば、まずは一つ目の場合分けについて答えが出たことになります。

数字を整理すると、頂点が定義域の中点よりも左側にある場合、つまり $a+1<5　⇔　a<4$ のとき、最大値は $-14a+35$ となります。

では次に、頂点が定義域の中点よりも右側にあるときを考えてみましょう。とは言っても改めて深く考える必要はなく、先ほどと同じようにイメージすればいいです。

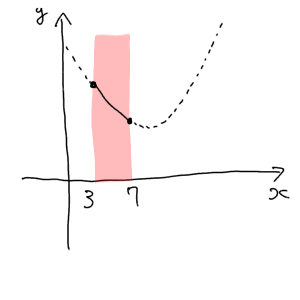
今度は定義域の左端が最大値になるだけです。数字を整理すると、頂点が定義域の中点よりも右側にある場合、つまり $a+1>5　⇔　a>4$ のとき、最大値は $f(3)=-6a+3$ となります。

ここまでの事をまとめると、最大値は

$a<4$ のとき $-14a+35$

$a≧4$ のとき $-6a+3$

となることがわかりました。ここで不等号に入れたイコールですが、これは $a<4$ に入れても $a>4$ に入れてもどっちに入れても良いです。

$a=4$ のとき、つまり頂点が定義域の中点にあるとき、最大値は定義域の左端・右端で等しくなるので、どっちに $a=4$ を代入しても同じ値になるからです。なのでお好みの所にイコールを入れて大丈夫です。

 

さあ、ここまでで最大値を求めることができたので、今度は最小値についてです。

最小値であっても、やはりグラフを頭の中で移動させてイメージすることによって、場合分けを理解することができます。ここまでの最大値についての話が理解できていれば、最小値の求め方もすぐにわかります。

 

最小値

最小値の場合、今度は三通りの場合分けをします。頂点が、定義域の左にあるか？中にあるか？右にあるか？の三つです。

1. 頂点が定義域よりも左側にあるとき

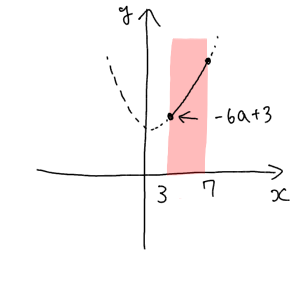
この場合は常に最小値が $x=3$ の点である $f(3)=-6a+3$ であることがわかりますね。よって $a+1<3　⇔　a<2$ のとき、最小値は $-6a+3$ となります。

 

2. 頂点が定義域の中にあるとき

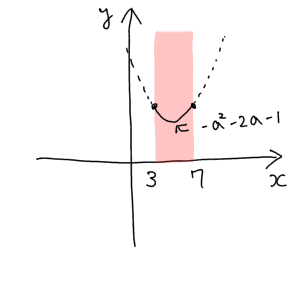
この場合は最小値が常に頂点となることがわかります。よって $3≦a+1≦7　⇔　2≦a≦6$ のとき、最小値は $-a^2-2a-1$ となります。

 

3. 頂点が定義域よりも右側にあるとき

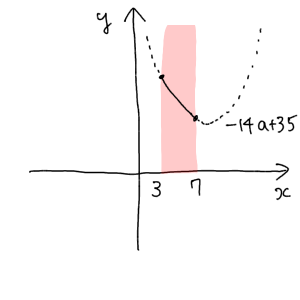
この場合は常に最小値が $x-7$ の点である $f(7)=-14a+35$ であることがわかります。よって $a+1>7　⇔　a>6$ のとき、最小値は $-14a+35$ となります。

さあ、これで全ての最大値と最小値のパターンが求まったので、いよいよ答える準備ができました。よって！答えは！

最大値は$\begin{eqnarray}\left\{\begin{array}{1}-14a+35　(a<4)\\-6a+3　(a≧4)\end{array}\right.\end{eqnarray}$

最小値は$\begin{eqnarray}\left\{\begin{array}{1}-6a+3　(a<2)\\-a^2-2a-1　(2≦a≦6)\\-14a+35　(a>6)\end{array}\right.\end{eqnarray}$

となります！お疲れさまでした。

 

 

定義域が動くパターン

しかし！まだまだあります！今度はなんと、定義域が動くパターン！！なんだか私もテンションが上がって参りました！

ただし！！定義域が動くといっても、なんら難しいことはありません。

さきほどグラフを頭の中で動かしてイメージしたように、今度は定義域を頭の中で動かせばいいのです。どっちが動いているかが違うだけであって、やることは全く一緒です。

・解説

二次関数の方はもう決定されていますから、なんとグラフが書けるんですね！これは親切！さっそく平方完成しましょう！！

$y=(x-2)^2+2$

そして間髪入れずにグラフを書く！

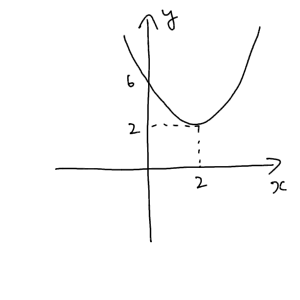
そして定義域を頭の中で左から右へと動かしていきます。まず最大値からイメージしていきましょう。

最大値

最大値については、やはり定義域の中点が二次関数の頂点よりも左側にある場合には、常に定義域の左端が最大値となることがわかります。

そして定義域の中点はというと、$\displaystyle\frac{(a-1)+(a+1)}{2}=a$ です。

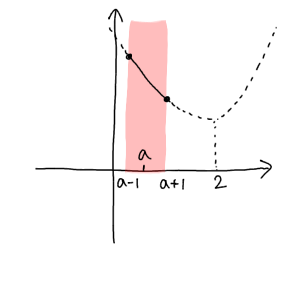
よって最大値は、$a<2$ のとき $y=(a-1)^2-4(a-1)+6=a^2-6a+11$

また、定義域の中点が頂点よりも右側にある場合には、今度は定義域の右端が最大値となることがわかります。

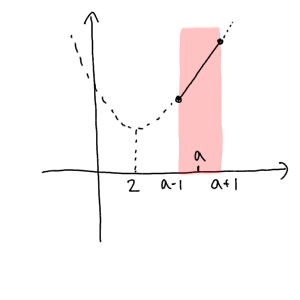
よって最大値は $a≧2$ のとき $y=(a+1)^2-4(a+1)+6=a^2-2a+3$ となります。

最小値

また、最小値についても、定義域を頭の中で左から右に動かしてイメージしていきます。そうすると、定義域が頂点よりも左側にある場合、最小値は常に定義域の右端であることがわかります。

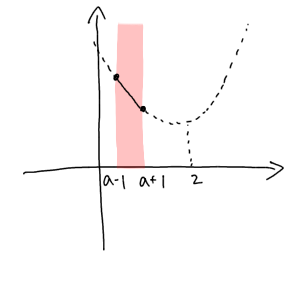
よって最小値は、$a+1<2　⇔　a<1$ のとき $y=(a+1)^2-4(a+1)+6=a^2-2a+3$

そして頂点が定義域の中にある場合には、頂点が最小値。

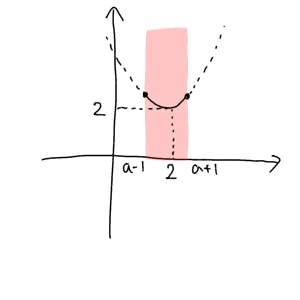
よって最小値は、$a-1≦2≦a+1　⇔　1≦a≦3$ のとき $y=2$

定義域が頂点よりも右側にあれば、最小値は常に定義域の左端です。

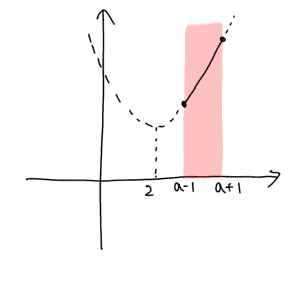
よって最小値は、$a-1>2　⇔　a>3$ のとき $y=(a-1)^2-4(a-1)+6=a^2-6a+11$

となります。まとめると

最大値は$\begin{eqnarray}\left\{\begin{array}{1}a^2-6a+11　(a<2)\\a^2-2a+3　(a≧2)\end{array}\right.\end{eqnarray}$

最小値は$\begin{eqnarray}\left\{\begin{array}{1}a^2-2a+3　(a<1)\\2　(1≦a≦3)\\a^2-6a+11　(a>3)\end{array}\right.\end{eqnarray}$

これで完成！

では最後に次の問題を。

 

そもそも二次関数じゃないパターン

・解説

まさかの四次式ですが、しかし焦らなくても大丈夫です。よく見てください。四次式ではあるものの、なんとなく二次関数っぽいですよね。

そう、こういう問題の時は、$x$ を何らかの形で置き換えて二次関数に持っていけばいいのです。

この場合であれば、仮に $x^2$ を $t$ と置き換えてみましょう。そうすると……

$y=x^4-2x^2-3$

$=t^2-2t-3$

二次関数になったッ！！！

こうやって、$x$ を別の文字で置き換えて、自分で二次関数に持っていくのです。ここまでくればあとは簡単に解けるでしょう。

ただし一つ注意点があります。今回、$x^2$ を $t$ と置き換えてみましたが、こういう風に自分で変数を定義する時は、解答中でしっかりそれを宣言する必要があるのです。

では例として実際のテストの答案っぽく答えを書いていきます。

 

・解答例

$x^2=t$ とおくと

$y=x^4-2x^2-3$

$=t^2-2t-3$

$=(t-1)^2-4$

また $y=0$ において

$t^2-2t-3=0$

解の公式より

$t=\displaystyle\frac {2\pm\sqrt{4-4\cdot(-3)}}{2}$

$=-1, 3$

よってグラフは次の通り。

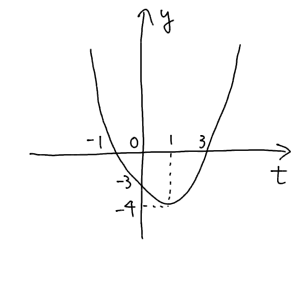
ここで $t=x^2≧0$ であるから、この範囲において $t=1$ のとき $y$ は最小値 $-4$ をとる。

このとき $x=\pm 1$

よって、$x=\pm 1$ のとき最小値 $-4$

 

・補足

なぜ $t≧0$ になるかというと、$x^2=t$ だからです。$x$ という実数を二乗したら必ず正の数になるので、$t≧0$ となります。この条件に注意してください。