連立不等式の解き方というのは、結局のところ、2つの不等式の共通範囲を求めればいいのです。なので一次不等式の解き方さえ分かっていれば連立不等式の問題も簡単に解けます。ここでは実際に問題を通して解き方をマスターしていきます。
問題
まずは上の不等式から解いていきます。
$3x+1>4+2x$
まずは数字の項を右辺にまとめて
$3x>3+2x$
最後に $x$ の項を左辺にまとめて
$x>3$
これでまず一つ目の不等式が解けました。次に二つ目の不等式を解いていきます。
$2x-8≦6$
数字の項を右辺にまとめて
$2x≦14$
両辺を $2$ で割って
$x≦7$
これで二つ目の不等式も解けました。二つの不等式を合わせて書くと
$x>3, x≦7$
この二つの不等式の共通範囲を求めれば連立不等式を解いたことになります。そして共通範囲を求めるコツは、とにかくグラフを書いて理解することです。グラフを書かないまま答えようとすると、慣れている人ですらミスを犯しやすいので、慣れていない内は特に、グラフを書くことをオススメします。
ではまず $x>3$ のグラフから書いてみます。
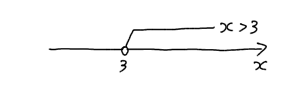
この上に $x≦7$ のグラフを重ねます。
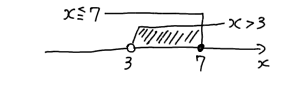
斜線で塗りつぶしている範囲が $x>3$ と $x≦7$ の共通範囲です。このグラフから、$x$ は $3$ と $7$ の間にあることがわかりました。
よって答えは
$3<x≦7$
となります。
連立方程式を解く時は、こうやって二つの方程式をグラフ(数直線)に書いていけば視覚的に理解できるのでミスを防げます。
ここでグラフの書き方について補足を。私の場合、不等号にイコールがあるかないかで書き方を分けています。
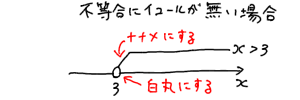
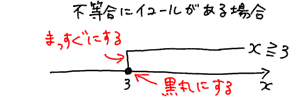
別に私と同じ通りに書く必要はありませんが、イコールが入っている場合と入っていない場合とでグラフの書き方を分けた方が混乱しにくくなります。自分の理解のためにも、何かしらの方法でイコールのある無しを書き分けた方が良いと思います。
では次の問題を。
問題
まず一つ目の不等式から解いていきます。
$2x+1>5$
数字の項を右辺に移動させて
$2x>4$
両辺を $2$ で割って
$x>2$
これで解けました。次に二つ目の不等式を解いていきます。
$3x+3≦2x+2$
数字の項を右辺に移動させて
$3x≦2x-1$
$x$ の項を左辺にまとめて
$x≦-1$
これで解けました。
この二つの不等式をグラフに書いて共通範囲を求めてみましょう。そうすると次のようになります。
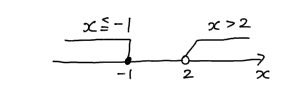
なんと共通範囲が無いんですね。よってこの場合の連立不等式は解なしとなります。
普通、計算問題というのは答えを求めさせるために出すものですから、解がある場合がほとんどです。しかし連立不等式の場合はこのように解なしとなるパターンもあるのです。なので、解が無いからといって不安になる必要はありません。連立不等式を解き、しっかりグラフを書いて、そのうえで解なしと判断できれば堂々と「解なし」と書けばよいのです。
こうやって「解なし」の場合に不安にならないためにも、やはりグラフはしっかり書いておくことをオススメします。
では次の問題を。
問題
式中に不等号が $2$ つ入っているパターンです。これはこのままイジッてはいけません。分解して連立不等式を立てるのが鉄則です。
$\begin{eqnarray}\left\{\begin{array}{1}2x+6<3x+8\\3x+8<5x+2\end{array}\right.\end{eqnarray}$
こういうふうに分解するんです。そうすれば今まで解いてきた連立不等式と同じノリで解くことができます。
まずは上の式から解いていきます。
$2x+6<3x+8$
数字の項を右辺に移動させて
$2x<3x+2$
$x$ の項を左辺に移動させて
$-x<2$
両辺にマイナスをかけて
$x>-2$
これでまずは一つ目の不等式が解けました。不等式にマイナスをかけると不等号の向きが逆になる事には常に注意してください。
では二つ目の不等式を解いていきます。
$3x+8<5x+2$
数字の項を右辺にまとめて
$3x<5x-6$
次に $x$ の項を左辺にまとめて
$-2x<-6$
最後に両辺を $-2$ で割って
$x>3$
これで二つ目の不等式が解けました。ここで二つの不等式の解をグラフに書いていきます。
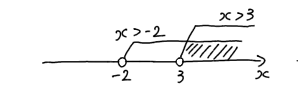
斜線で塗りつぶされている部分が共通範囲です。よって解は $x>3$ となります。
では最後に少し応用を利かせた問題を。
問題
まずは連立不等式に分解します。
$\begin{eqnarray}\left\{\begin{array}{1}x+2a+1>3x+1\\3x+1>x+7\end{array}\right.\end{eqnarray}$
では一つずつ解いていきます。まずは上の不等式から。
$x+2a+1>3x+1$
両辺から $1$ を引いて
$x+2a>3x$
$x$ の項を左辺、$a$ の項を右辺に移動させて
$-2x>-2a$
両辺を $-2$ で割って
$x<a$
これでまずは一つ目の不等式の解が求まりました。次は二つ目の不等式を。
$3x+1>x+7$
数字の項を右辺、$x$ の項を左辺に移動させて
$2x>6$
両辺を $2$ で割って
$x>3$
これで連立不等式の解が求まりました。これをグラフに書いていきます。
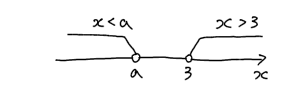
問題は「解を持たないとき」とあります。なので、この二つのグラフが共通範囲を持たないような $a$ の値を考えればいいです。どう考えればいいかというと、$a$ の値はまだ決まっていないので、$a$ を頭の中で自由に動かしてみるんです。
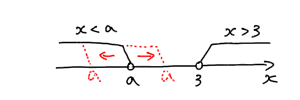
そして右に動かしていくと、$a>3$ の場合でこの連立不等式が共通範囲を持ってしまう事がわかります、このように。
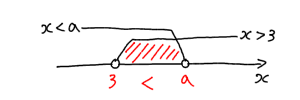
これでは解を持ってしまうことになります。なので $a$ は $3$ より小さくなければいけません。
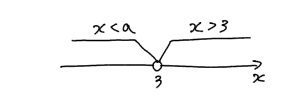
これでちょうど連立方程式がギリギリ解を持たない範囲を決めることができました。よって
$a≦3$
が答えとなります。
ここで不等号のイコールについてですが、$x>3$ には $3$ が含まれていないので、$a$ に $3$ を含めても解なしを達成できる。なので答えの不等号にもイコールを入れた $a≦3$ が正解です。