重複組み合わせは絵を描けば理解できる。イラストで解説

重複組み合わせとは

その名の通り、重複オッケーな組み合わせ問題のことです。と説明しても曖昧で分かりづらいと思うので、いきなりですが具体的な問題を例にとって考えていきたいと思います。

たくさんある中から選ぶので、たとえば「りんご、りんご、りんご、みかん」のように、りんごを重複して買うこともできるんですね。これが重複組み合わせです。

問題なのは、これをどうやって計算するか？ということです。

重複組み合わせを解くには、とにかくイラストで理解するのが一番の早道です。これ以外に方法が無いです。

まず「4個買う」という条件は確定しているので、これをイラストで表してみます。

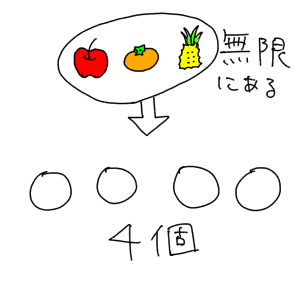
下に描いた4つのマスの中に、りんご・みかん・パインのいずれかが入るわけです。そして、その果物の種類の違いを仕切りで表現してみるんです。

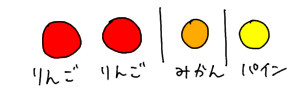
そうすると、この「4つのマス」と「2つの仕切り」の組み合わせで、問題の場合の数がすべて表現できるんです。

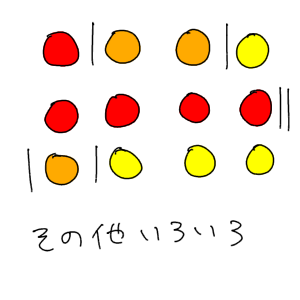
果物の種類が違うところに仕切りを入れる。もし全部がりんごなら、2つの仕切りを右端に寄せればいい。

こういうふうに考えていくと、重複組み合わせ問題というのは、つまりこのマスと仕切りの計6個の組み合わせ問題であるという事に帰結します。

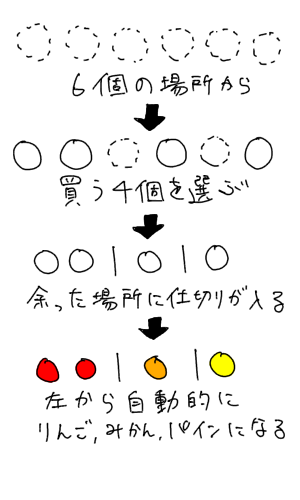
6個の場所から4個を選べば、あとは自動的に仕切りが入るし、自動的にりんご・みかん・パインも入る。こういう考え方です。

なので計算は$_6C_4=_6C_2=\displaystyle\frac{6\cdot 5}{2\cdot 1}=15$通り

これが重複組み合わせの解き方です。

もしくは6個の場所から2個の仕切りを選ぶ、と捉えても良いです。上の計算で見たように$_6C_4=_6C_2$ですから、結果は同じになります。自分にとって分かりやすい方法で理解してください。

ここで補足ですが、今回は左から順にりんご→みかん→パインと入れましたが、この順番はどう入れ替えても良いです。パイン→りんご→みかんでも、何でもいいです。

何が言いたいかというと、並べ替えのパターンをも考える必要はない、ということです。

今回は説明のために便宜上1列に並べて表現しただけであって、この問題はあくまで「取り出す」だけの組み合わせの問題です。並べる必要はないので、順番は気にしなくてもいいんですよ、ということです。

重複組み合わせの公式

上の例では3種類の果物の中から4個選ぶという計算をしました。その結果、$_6C_4$という式ができました。

これは$_{4+(3-1)}C_4$と表せます。

左側は、4個の選ぶべきマスに加えて3-1個の仕切りが入り、計4+(3-1)の場所ができた、という意味です。

これをより一般化した公式は次のようになります。

$_{n+r-1}C_r$

また、この重複組み合わせの計算を特に$H$として表すこともあります。

$_{n+r-1}C_r=_nH_r$

まあ$_nH_r$と表したところで結局$_{n+r-1}C_r$に分解して計算することになるわけですし、なぜ$_{n+r-1}C_r$という計算になるのかを理解するにはやはり上でやったように「マス」と「仕切り」の考え方で問題を整理することが必要になってくるので、慣れない内はとにかくマスと仕切りを描いて問題を解いてみることをオススメします。

では更にいくつか問題を解いてみて重複組み合わせの解き方を解説していきます。

重複組み合わせの問題

思わず箱のほうをマスに当てはめそうになりますが、そうするとボールが溢れてしまいます。ここはボールをマスに当てはめるべきです。

そして仕切りの数は、3個の箱が表せられればいいので、3-1=2個の仕切りで表現できます。

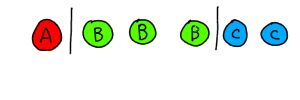
こういう解釈です。そうすると「8個の場所から6個のマス（or 2個の仕切り）を選ぶ」という組み合わせとして計算できるので

$_8C_6=_8C_2=\displaystyle\frac{8\cdot 7}{2\cdot 1}=28$通り

となります。

では次は少し応用的な問題を。

一見難しそうですが、なんてことはないです。$x$がりんご、$y$がみかん、$z$がパインだと思えばいいですから。そうすれば始めに解いた問題と似たような解き方で解けることがわかります。

ただし！今回の条件は「正の整数解」とあります。つまり0は含められないので、そこを工夫する必要があります。

どうすればいいのかというと、これは結論から言うと解き方のアプローチは2つあります。どちらも紹介するので自分にとって納得のいく方法で解いてみて下さい。

1つ目のパターン

まず、最低でも$x,y,z$は$1$以上でなければならない（＝りんご、みかん、パインを最低でも一個買わなければならない）と考えるんです。

$(x,y,z)=(1,1,1)$が最低条件であるならば、それをあらかじめ引いておけばいい。そうすると「$x+y+z=6$の$0$以上の整数解を求める問題」と読み替えることができます。

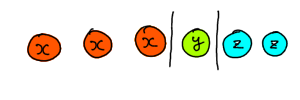
ここまで解釈できれば、あとはこれを計算するだけ。8個の場所から6個のマス（or 2個の仕切り）を選ぶ解き方です。

$_8C_6=_8C_2=\displaystyle\frac{8\cdot 7}{2\cdot 1}=28$通り

これでできました。

2つ目のパターン

$x+y+z=9$という方程式を、そのまま素直にマスに当てはめる解き方です。そうすると、0という数はとれない＝両端に仕切りが来ることはできない、という問題に読み替えることができます。

これまでの問題であれば、9個のマス＋2個の仕切り＝計11個の場所を描いて、そこから9個のマスを選ぶ、という解き方をしてきましたが、これでは両端に仕切りが入る余地があるので、まず2個の仕切りを場所から除くんです。

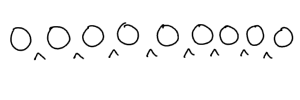
そして、9個の場所の隙間から2個の仕切りを選ぶ問題であると読み替えるんです。こうすれば両端に仕切りが来るケースを排除できます。

隙間の合計は8箇所です。この中から2箇所、仕切りを入れる所を選べばいいので

$_8C_2=\displaystyle\frac{8\cdot 7}{2\cdot 1}=28$通り

となります。