重複順列とは
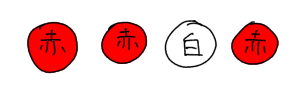
↑このように同じものを並べられる順列のことを重複順列といいます。上の例で言えば、「赤」という同じボールが3つ並んでいますよね。こうやって重複して並べられる順列のことです。
通常の順列であれば同じものを並べることができません。たとえばA、B、C、Dの4人を一列に並べるとしたらこんな感じになるわけです↓
ちょっと不気味な絵ですが、普通の順列というのはこのように重複することができないものです。
でも重複順列なら同じものが並べられる!ヤッター!全然嬉しくないけど、これが普通の順列と重複順列の違いです。そして重複順列の計算方法は、普通の順列の計算方法とは少し異なります。
例題を通して解き方を確認してみましょう。
重複順列の計算
問題
箱が4つということで、まずイラストを描いてみます。
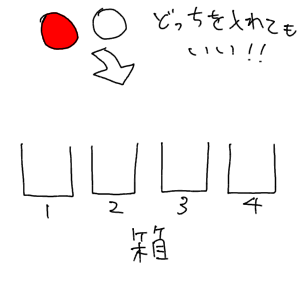
ここでポイントとなるのは、赤・白のボールの個数は指定されていないということです。無限にあるわけですね。そしてその無限にあるボールの中から赤・白を選んで箱に入れていく。
無限にあるので、同じものを入れても良いんです。重複してもいい。
そうすると、1の箱に入れられるボールの場合の数は、赤と白の2通り。2の箱に入れられるボールの場合の数も2通り。3の箱も、4の箱も同様。
となると計算は
$2^4=2\cdot 2\cdot 2\cdot 2=16$通り
となります。イラストで表すとこういう感じです↓
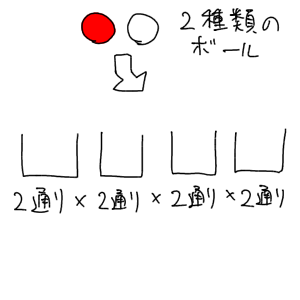
重複順列は、このように累乗(べき乗)で計算するのが特徴です。
一方で重複順列の問題というのは、その問題が重複順列であるということを見抜けるかどうかが少し難しく、やっかいな問題でもあります。しかしこれは慣れれば何てことないです。
パターンを見抜くためにいくつかの例題を解いていきましょう。
重複順列を見抜く
問題
こういうパターンですね。ここでたとえば、1個取り出すとき、2個取り出すとき……と場合分けして計算してもいいのですが、それだと結構な時間がかかってしまいます。
そこで、問題の切り口を変えてみるんです。具体的には「取り出す」という操作に着目してみます。
そうすると、あるボールについて、「取り出す」と「取り出さない」の2通りの操作を当てはめることができるんです。ということは!ここで重複順列の解き方に持っていけるんですね。
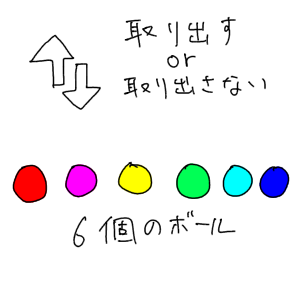
6個のボールそれぞれについて、「取り出す」と「取り出さない」の選択肢がある。これを計算すると
$2^6=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2=64$通り
これで計算できましたが、しかし!問題では「少なくとも1個取り出す」と書かれていることに注意です。
計算した$64$通りの中には「すべて取り出さない」という場合も含まれているので、これは「少なくとも1個取り出す」という条件を満たしません。なので、この1通りだけ除外する必要があります。
$64-1=63$通り
これで完成!
重複順列の問題は、このように操作方法について場合の数を計算することを言うんですね。そうすることによっていちいち場合分けをするよりも楽に計算できるんです。
なので、重複順列を見分けられるかどうかで計算時間が大幅に変わってきて、試験でも素早く解けるようになるので、ぜひ解き方をマスターしてみて下さい。
練習のためもう少し例題をやってみましょう。
組分けの問題
問題
さきほどと同じノリで解けます。6個のボールそれぞれについてA、Bの2通りの分け方があるので、計算は
$2^6=2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2=64$通り
となると思いきや、しかし!この計算では全部のボールがAになってしまうパターンと全部のボールがBになってしまうパターンが含まれています。その場合は2組に分けられていないので問題の条件を満たさないことになってしまいます。
そのため、全部Aパターンと全部Bパターンの計2通りを引くことが必要です。
$64-2=62$通り
これで完成!こういうのを「組分けの問題」とか言ったりします。さあ次の問題!
問題
はいはい重複順列の組分けパターンね、じゃあ計算はっと
$2^5-2=2\cdot 2\cdot 2\cdot 2\cdot 2-2=30$通り
はいできた。と思った方もいるかもしれません。が、しかし!
この問題の場合はグループの区別がついていないんです。ひとつ前の問題はグループがA、Bと区別されていましたが、この問題の場合は区別の指定は無い。
つまり、たとえば仮に5人にそれぞれ番号を振って12345のゼッケンをつけたとして、グループに分けたとすると、「123」「45」の分け方と「45」「123」の分け方は同じになってしまうんです。
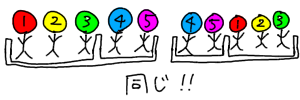
なので、計算で求めた30通りはグループの区別がついている場合の数なので、区別が無いときは2で割る必要があります。
$30\div 2=15$通り
これで完成!
組分けの問題はこうやって、「0人のグループが許されるか?」ということと、「グループ同士の区別がついているか?」に注意して解いていけばオッケーです。