不等式の考え方は至ってシンプル。
$a>b$
という式があったとしましょう。この式が意味しているものは「 $a$ は $b$ よりデカい」これだけです。これ以外の何物でもないです。不等式は結局のところこの考え方に尽きるんです。
そして不等式にはもう一つの記号があります。
$a≧b$
この式が意味しているものは「 $a$ は $b$ よりデカい、ただし $a=b$ の場合もあり」ということです。両辺が同じ値を含んでいるかどうかで $>$ と $≧$ を使い分けます。
これが不等式の考え方です。これさえ踏まえておけば何も怖くないです。
では具体的な不等式の扱い方を実際の計算問題を通して体に刻みつけていきましょう。
問
$x-1$ の値を知りたいので、すべての辺から $1$ を引けばよいです。
$-1<x≦2$
$⇔-2<x-1≦1$
これで完成。求めたい値になるように足し算引き算をすればいいのです。
では次の問題です。
問
これも先ほどと同じようにすればよいです。
$2x$ の値が知りたいので、$x$ に $2$ をかける。
$3<x<5$
$⇔6<2x≦10$
これで完成。求めたい値になるように掛け算割り算をするんです。
では次の問題です。
問
さあ早速 $-2$ をかけてみましょう……と言いたいところですが、マイナスをかけるのは注意が必要です。
不等式には、マイナスをかけると不等号の向きが反対になるという性質があります。
そのため、この問題の場合には、$-2$ をかけると同時に不等号の向きを逆にする必要があります。
$1<x<3$
$⇔-2>-2x>-6$
$⇔-6<-2x<-2$
これが正解です。
ちなみに最後、不等号の向きを問で与えられた向きと同じになるように揃えてみましたが、これは別にやってもやらなくてもどちらでもいいと思います。数学的に意味は同じなので気にする必要はないです。ただこういう見た目をイチイチ気にするのが理系なのでそこはカンベンしてください。
そして、ここからが肝心の話です。「なぜマイナスをかけると不等号の向きが逆になるのか?」ということです。
これは数直線を書いてみれば直感的に理解できます。
まずは不等式をいったん脇において、ただの数について考えてみましょう。
例として $x$ の数直線上に $3$ を記入してみます。
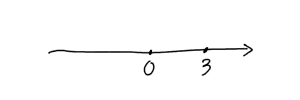
そしてこれにマイナスをかけてみます。$3$ にマイナスをかけると $-3$ になりますよね。$3$ にマイナスをかけて $-3$ にした結果、数直線上で何が起こるかというと、こうなるんです。
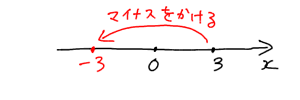
こうやって原点をまたいで反対側に移動したんですね、$3$ が。
数にマイナスをかけるということは、その数が数直線の反対側に移動することを意味します。
ここで再び不等式に戻ってみましょう。例として $x>3$ の不等式を数直線で表現してみます。
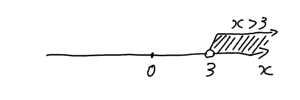
マイナスをかけると、この範囲が原点をまたいで反対側に移動するんです。
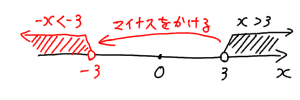
$x$ が $3$ より大きいならば、$-x$ は $-3$ より小さくなる。つまり $x>3$ にマイナスをかけると $-x<-3$ になる。だから不等号の向きを逆にしないといけないんです。
この「マイナスをかけたら不等号の向きを逆にする」という操作は不等式の問題を解くにあたって絶対に守るべきルールなので、マイナスをかける時は常に忘れずに逆向きにしてください。
また同様の理由で、マイナスで割るときも逆にしてください。たとえば -$3$ で割るということはつまり $-\displaystyle\frac{1}{3}$ をかけることに等しいわけですから、マイナスにすべきです。
では最後にまとめの問題を解いていきましょう。
問
今こそこの記事で学んできたすべての知識をフル活用する時です。ゴリゴリ計算を進めていきます。
$-2<x<1$
$⇔-4<2x<2$
また
$-3≦y<2$
$⇔9≧-3y>-6$
$⇔-6<-3y≦9$
よって
$-10<2x-3y<11$
$⇔-9<2x-3y+1<12$
これで解けました。
途中、$x$ の項と $y$ の項を足し合わせる段階で不等号のイコール記号が取れて $≦$ から $<$ になりました。ここで悩んだ方もいるかもしれません。これはそれぞれの項の最大値を実際に書き出してみればわかります。
$2x$ の最大値は $1.9999999……$ であり、$-3y$ の最大値は $9$ です。両者を足し合わせると $10.9999999……$ であり、ギリ $11$ に届かないので、不等号のイコールは外すのが正解です。