$\require{cancel}$
順列の公式を憶えること自体はそこまで難しくないと思われます。ポイントは、公式をいかに使いこなすか?ということです。
そのためには、何よりもまず、公式の意味していることをイメージで理解する必要があります。
この記事では例題と共に公式の使い方を解説していきますが、併せて公式を図で表しイメージする方法も解説します。
はじめに:順列の公式の確認
$n$個の物の中から$r$個を取り出して一列に並べたものを順列といい、その並べ方の総数は
$_nP_r=\displaystyle\frac{n!}{(n-r)!}$
と表せます。
使用例:10個の異なるボールが入った箱から3個のボールを取り出して一列に並べる場合
その並べ方の総数は
$_{10}P_3=\displaystyle\frac{10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=\displaystyle\frac{10\cdot 9\cdot 8\cdot \cancel{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}}{\cancel{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}}=10\cdot 9\cdot 8=720$
となります。公式をそのまま使うと、このように$7$から下がすべてキャンセルされるので、はじめからキャンセルすることを想定して次の形で表した公式が便利です。
$_nP_r=\displaystyle\frac{n!}{(n-r)!}=n(n-1)(n-2)・・・(n-r+1)$
ただ、この公式を見ただけでは、はじめは一体何のことだか分からないかもしれません。公式を理解するには、順列をイメージで理解することが必要です。
順列の公式をイメージで理解する
再び先ほどの例に戻ってみましょう。
例:10個の異なるボールが入った箱から3個のボールを取り出して一列に並べる場合
これを図に表してみます。10個のボールを一列に並べるので、その並べた状態を3個のマスに置き換えてみます。
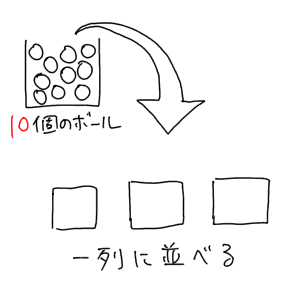
左のマスから順番に埋めていきましょう。このとき、はじめは10個のボールがありますから、左のマスに入りうるボールは10通りあることになります。そして、10通りあるボールの中から1つを選んで左のマスを埋めた結果、残りのボールは9個に減りました。
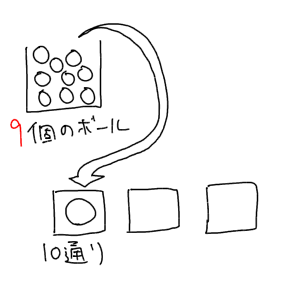
次に真ん中のマスを埋めます。残りのボールは9個なので、真ん中のマスに入りうるボールは9通りになります。そして真ん中のマスを埋めた結果、残りのボールは8個に減りました。
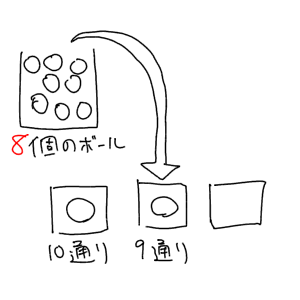
最後に右のマスを埋めます。残っているボールの数は8個なので、右のマスに入りうるボールは8通りです。ということは!
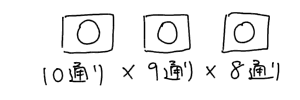
最終的にこうなるわけですね。だから計算は$10\cdot 9\cdot 8$となるわけです。これを公式と照らし合わせると
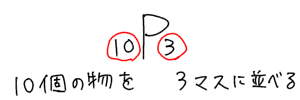
こういう感覚です。そして、並べていくごとに1個ずつ減っていく。だから$10\cdot 9\cdot 8$になる。こういう感覚で公式を理解してください。
では実際に例題を通して公式を活用してみましょう!
問題
解説
AとBが隣り合うので、二人はずっと一緒にいるんですね。ということは、この二人を1セットとして考えればいいのです。こんな感じで↓
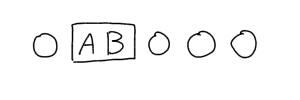
そうすると、実際には5個の順列を計算すればいいことがわかります。ただし!AとBのセットには、BAのパターンもあります。
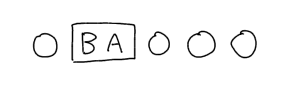
つまり、ABのセット自体にも2個の順列があるんです。ということは、5人の順列×2人の順列、という計算をすればいいことがわかります。よって
$_5P_5\times _2P_2=120\cdot 2=240$通り
問題
解説
まず男子の並び方は特に指定は無いので、男子から並べていきます。そして、その男子の隙間のどこに女子を入れていけばいいか?と考えればよいです。

この○の中に女子が入るイメージです。そして「女子2人が隣り合う」のが条件なので、やはりここでも2人を1セットとして考えます。そうすると、女子1人の枠と、女子2人1セットの枠の、計2枠をどこに入れるか?という問題になります。
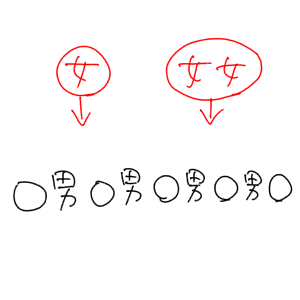
以上を踏まえると、この計算に必要な順列は3つあることがわかります。
・女子3人から2人を選ぶ順列:$_3P_2$
・男子の隙間5枠から、女子を入れる2枠を選ぶ順列:$_5P_2$
・男子4人の順列:$_4P_4$
これらを掛け合わせたものが全ての順列の総数になります。よって
$_3P_2\times _5P_2\times _4P_4=6\cdot 20\cdot 24=2880$通り