組み合わせ＝並べない順列のこと。考え方と計算方法を解説

組み合わせとは

「並べない順列」というのも少し日本語がおかしいですが、つまり組み合わせとは「選ぶだけ」の場合の数の事を言うんです。

たとえば順列が「7個のボール中から→3個選んで→1列に並べる」という場合の数を数えたのに対し、組み合わせは「7個のボールの中から→3個を選ぶ」という場合の数だけを数えるんです。

これが順列と組み合わせの違いです。

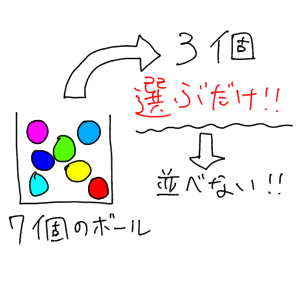
そういう意味で、組み合わせとは「並べない順列」と言えます。

順列を学んだ後ならついつい並べたくなる気持ちはわかりますが、組み合わせでは並べないんです。寸止めするんですね。並べる手前でグッと堪えてください。

そして組み合わせの計算方法は、順列の計算方法がわかっていれば簡単に理解できます。

組み合わせの計算方法

上の例で言うと、もしこれが順列なら、7個のボールから3個を選んで一列に並べる順列は$_7P_3$と計算していました。

しかしこれは「7個から3個選ぶ場合の数」×「3個を一列に並べる場合の数」が合わさった数字です。

ということは、組み合わせなら「並べるだけ」ですから、つまり$_7P_3$から「3個を一列に並べる場合の数=$3!$」を割ればいいんですね。

そうすると

$\displaystyle\frac{_7P_3}{3!}=\displaystyle\frac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1}=35$

これが組合せの解き方です。

組み合わせの公式

より一般化した公式は次のようになります。$n$個のものの中から$r$個を選ぶとき、その組合せの数は

$_nC_r=\displaystyle\frac{_nP_r}{r!}$

と表せます。先ほどのボールの例で言うと、$n=7$、$r=3$だったんですね。

順列を$P$（permutation）で表したのに対し、組み合わせは$C$（combination）で表します。

では早速、公式を使いこなすために、いくつか例題を解いていきましょう。

$\require{cancel}$

組み合わせの問題

もはや公式を使ってくださいと言わんばかりの問題です。さっそく当てはめていきます。

$_8C_6=\displaystyle\frac{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3}{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=\displaystyle\frac{8\cdot 7\cdot \cancel{6\cdot 5\cdot 4\cdot 3}}{\cancel{6\cdot 5\cdot 4\cdot 3}\cdot 2\cdot 1}=\displaystyle\frac{8\cdot 7}{2\cdot 1}=28$通り

これで求まりました。

が、しかし！求まったのは良いのですが、途中で約分されている数字が結構あるのが分かるかと思います。

そして最後の方を見ると、$\displaystyle\frac{8\cdot 7}{2\cdot 1}$となっています。これは$_8C_2$と同じですよね。

そう、組み合わせの公式には、このように$_8C_6=_8C_2$と換算できる性質があります。これを利用すれば計算が少し楽になります。

より一般化した公式で表すと

$_nC_r=_nC_{n-r}$

と表せます。

たとえば$_{13}C_{11}$みたいに、右側の数字が大きいときは、この性質を利用して$_{13}C_2$と変形すれば、計算を楽にすることができます。積極的に利用していきたい性質です。

もう少し例題をやってみましょう。

$_7C_3=\displaystyle\frac{7\cdot 6\cdot 5}{3\cdot 2\cdot 1}=35$個

もはや一瞬で計算できる。

組み合わせなので、こうやって図形と絡めた問題が出されることも多いです。

では次は順列でも少しやった「組分け」の問題をやってみます。

9人から4人選ぶのは$_9C_4$通り、残りの5人から3人を選ぶのは$_5C_3$通り、残りの2人から2人を選ぶ方法は1通り。よって

$_9C_4\times _5C_3=\displaystyle\frac{9\cdot 8\cdot 7\cdot 6}{4\cdot 3\cdot 2\cdot 1}\times\displaystyle\frac{5\cdot 4}{2\cdot 1}=126\cdot 10=1260$通り

となります。