二次関数の理解はグラフの理解から始まります。そしてグラフさえ理解していればあらゆる二次関数の問題が簡単に解けるようになります。
ここでは以下の問題を例にして、二次関数のグラフを描くために必要な全ての手順を徹底解説していきます。
問題
それでは早速解いていきましょう。始めに整理しておくと、二次関数のグラフを書くにあたって必要な情報は以下の3つです。
・頂点の座標
・グラフの向き(上に凸か下に凸か)
・軸との交点
これを求めていきます。
まずは平方完成する
全ての二次関数は、それを平方完成した形 $y=a(x-p)^2+q$ に表すことができます。そしてこの形にすることによって2次関数の頂点の座標と凸の方向を求めることができます。
平方完成はグラフを書くために必要な作業なので絶対にマスターしておきましょう。はじめは時間がかかると思いますが、慣れるとアッという間にできるようになります。
では平方完成をしていきます。
$y=2x^2-12x+14$
$=2(x^2-6)x+14$
$=2(x^2-2\cdot3x)+14$
$=2\{(x-3)\cdot(x-3)-9\}+14$
$=2\{(x-3)^2-9\}+14$
$=2(x-3)^2-18+14$
$=2(x-3)^2-4$
これでグラフを書くために必要な形にすることができました。今回は一つ一つの手順を細かく書いていきましたが、慣れると十秒くらいで平方完成できるようになるので、色々な問題で手を動かしてトレーニングしてみて下さい。
次に頂点と凸の方向を読み取る
一般に、$(p, q)$ の頂点を持つ二次関数は、先ほど示した形
$y=a(x-p)^2+q$
で表すことができます($a$ は定数)。そして、$a$ がプラスであれば下に凸、マイナスであれば上に凸のグラフになります。これを踏まえて、先ほどゲットした式
$y=2(x-3)^2-4$
と照らし合わせてみましょう。そうすると $p=3$、$q=-4$ と対応しているため、頂点の座標は$(3, -4)$ であることがわかりました。
また、$a=2$ であり、つまりプラスなので、このグラフは下に凸であることもわかりました。
補足:凸とは?
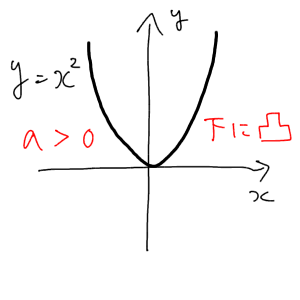
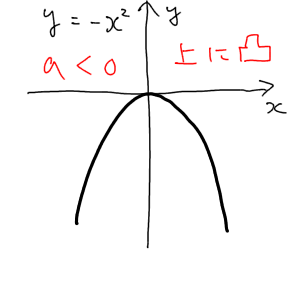
二次関数のモッコリ感のことです。下にモッコリしていれば下に凸、上にモッコリしていれば上に凸と言います。もし $a$ がプラスかマイナスかでグラフはどっちに凸だったかな?と忘れた時は二次関数の原型 $y=x^2$ に立ち返ってみて下さい。$y=x^2$ のグラフであれば下に凸であったことがすぐに思い出せるはずです。この時 $a$ は $1$、つまりプラスなので、ということは $a$ がプラスであれば下に凸だ、と思い出してください。
軸との交点を求める
まずは $x$ 軸との交点から求める
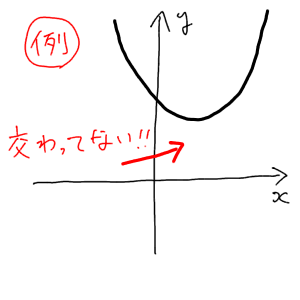
軸との交点を求めるにあたって、まずはグラフが $x$ 軸と交わっているかどうか?を判断する必要があります。もし $x$ 軸と交わっていなければ、そもそも $x$ 軸との交点を求める必要がありませんからね。
今回のグラフは頂点の座標が $(3, -4)$、つまり $y$ 座標がマイナスであるため、頂点は $x$ 軸よりも下にあることがわかっています。そして $a$ がプラスであるため、下に凸=上に伸びたグラフであることもわかっています。
ということはこの二次関数のグラフは $x$ 軸との交点を持つグラフなので、 $x$ 軸との交点の座標を求める必要があることがわかります。
もし上手くイメージできなければ、この段階で一旦ラフスケッチをしてみると良いでしょう。 $x$ 軸との交点を持つことが視覚的に理解できると思います。
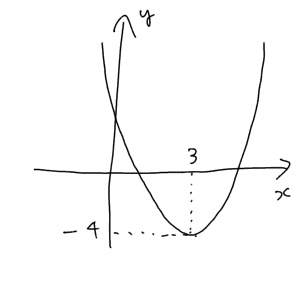
$x$ 軸との交点を求めるにあたっては、まず一旦、問で与えられた形式に立ち返ってみます。
$y=2x^2-12x+14$
ここからどのようにして $x$ 軸との交点を求めるか?それは $x$ 軸の性質を考えてみればわかります。$x$ 軸とはそもそも$y=0$を通る直線のことです。つまり、$x$ 軸との交点を求めるということは二次関数に $y=0$ を代入した二次方程式を解くことに等しいんです。
では問題の二次関数に $y=0$ を代入してみましょう。
$2x^2-12x+14=0$
この二次方程式を解く方法は
・因数分解する
・解の公式を使う
の2通りあります。どちらでも良いのですが、ここでは確実を期して解の公式を使って解いていきます。
というのも、もし解に分数やルートが入っている場合、ややこしくて因数分解ができなくなってしまい、本番の大学入試でパニクる可能性があるので、常に解の公式で解く覚悟を決めた方がいいと個人的には思います。
毎回毎回、楽に因数分解できるとは限りませんからね。たまたまスッと因数分解を思いついたらラッキー、ぐらいの気持ちでいくのがいいと思います。
では解の公式を使って解いていきましょう。問題の二次関数に $y=0$ を代入した式をもう一度示すと
$2x^2-12x+14=0$
です。まず両辺が $2$ で割れることに気付くので、$2$ で割ってシンプルな形にします。
$x^2-6x+7=0$
ここから解の公式 $x=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ に代入していきましょう。
$x=\displaystyle\frac {-b\pm\sqrt{b^2-4ac}}{2a}$
$=\displaystyle\frac {-(-6)\pm\sqrt{(-6)^2-4\cdot1\cdot7}}{2\cdot1}$
$=\displaystyle\frac {6\pm\sqrt{36-28}}{2}$
$=\displaystyle\frac {6\pm\sqrt{8}}{2}$
$=\displaystyle\frac {6\pm2\sqrt{2}}{2}$
$=3\pm\sqrt{2}$
よって $x$ 軸との交点は $x=3+\sqrt{2}$, $3-\sqrt{2}$ であることがわかりました。
次に $y$ 軸との交点も求める
$y$ 軸は $x=0$ と表せるので、二次関数に $x=0$ を代入した方程式を解けばよいです。問題の二次関数であれば$y=2x^2-12x+14$、これに $x=0$ を代入して$y=14$となります。これが $y$ 軸との交点です。超簡単。
グラフを書く
ここまでに得た情報を整理すると以下のようになります。
・頂点の座標は $(3, -4)$
・グラフは下に凸
・$x$ 軸との交点は $x=3+\sqrt{2}$, $3-\sqrt{2}$
・$y$ 軸との交点は $y=14$
ここまでわかれば後は書くのみです。
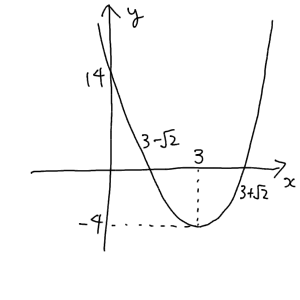
これで完成!100点!
いや実はちょっと画像の作成に手間取ってしまって縮尺がおかしいんですけれども、だいたいこんなもんでしょう!やっぱ90点!
補足:二次関数の平行移動
先ほど出てきた平方完成の結果式 $y=a(x-p)^2+q$ ですが、これを見て疑問に思った方もいるかもしれません。なぜ $p$ と $q$ とでプラスとマイナスがごっちゃになっているのか?これを理解するためにはグラフの平行移動について知っておく必要があります。
結論から言うと、グラフの頂点を $(p, q)$ 平行移動させたければ、$x$ に $x-p$、$y$ に $y-q$ を代入すればよいのです。二次関数であれば、その基本形
$y=x^2$
これを $(p, q)$ 平行移動させると
$y-q=(x-p)^2$
となります。そしてこれを $a$ だけ絞れば
$y-q=a(x-p)^2$
になります。
つまり二次関数というのは全て基本形 $y=x^2$ からの派生なんです。
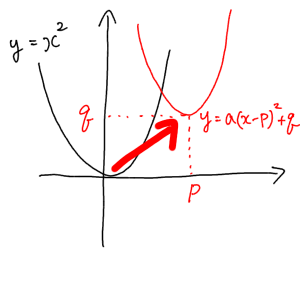
$y=x^2$ の頂点を $(p, q)$ 平行移動させるには、移動後でも両辺が釣り合うようにするために、あらかじめ $x$ から $p$ 、$y$ から $q$ を引いておく。そして絞り具合を表現するために $a$ をかける。こういう感覚で覚えておくとよいです。
つまり全ての二次関数は、本来は $y-q=a(x-p)^2$ の形で表されるんです。それを見やすくするために $y=$ の形に直してるだけ。こう理解して下さい。
$p$ と$q$ とでプラスとマイナスがごっちゃになっているのはこのためです。
もし $y=a(x-p)^2+q$ を思い出そうとしたとき、プラスとマイナスがどっちか忘れたら、上記のように常に二次関数の基本形 $y=x^2$ に立ち返ってみて下さい。
そしてその頂点を $(p, q)$ だけ平行移動し $y-q=(x-p)^2$ にする。そしてそれを $a$ だけ絞って $y-q=a(x-p)^2$ にする。最後に見やすくするために $y=a(x-p)^2+q$ にする。
こうやって自力で導出できるようになればプラスとマイナスで混乱することが無くなるはずです。
ちなみにこの $(p, q)$ 平行移動させたい時に、$x$ に $x-p$ 、$y$ に $y-q$ を代入するという作業は、二次関数に限らず全ての関数で使うことができます。もし大学入試で「グラフを $(4, -7)$ 平行移動させろ!」と言われたら即座に $x$ に $x-4$、$y$ に $y+7$ を代入する。これであらゆる関数を平行移動させることができます。